We take the first equation {eq}x^2 y^2 w^2 z^2 = 1 {/eq} and take the partial derivative wrt x with z as a constant, as denoted in the See full answer belowSecond derivative of sin^2;Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music
Solved Find All The First And Second Order Partial Derivatives Of F X Y X 2y 2 E Xy Sin X 2y Course Hero
X/(x^2 y^2) partial derivative
X/(x^2 y^2) partial derivative- 1 Find all the 1 st order partial derivatives of the following function f (x,y,z) = 4x3y2 −ezy4 z3 x2 4y −x16 f ( x, y, z) = 4 x 3 y 2 − e z y 4 z 3 x 2 4 y − x 16 Show Solution So, this is clearly a function of x x, y y and z z and so we'll have three 1 st order partial derivatives and each of them should be pretty easy toSo in the last couple videos I talked about partial derivatives of multivariable functions and here I want to talk about second partial derivatives so I'm going to write some kind of multivariable function let's say it's I don't know sine of X times y squared sine of X multiplied by Y squared and if you take the partial derivative you have two options given that there's two variables you can



Solved Determine The Second Partial Derivatives Of F X Y Z Tan 5 2x2y4z2 Xx 4y42 8x2y422tan 2x2y422 5 1 Sec 2x2y4 2 5 Course Hero
3 If z = f(x,y) = xexy, then the partial derivatives are ∂z ∂x = exy xyexy (Note Product rule (and chain rule in the second term) ∂z ∂y = x2exy (Note No product rule, but we did need the chain rule) 4 If w = f(x,y,z) = y xyz, then the partial derivatives are ∂w ∂x = (xy z)(0)−(1)(y) (xy z)2 = −y (xy z)2 (Note Quotient Rule) ∂w ∂y = (xy z)(1)−(1)(y)Free derivative calculator differentiate functions with all the steps Type in any function derivative to get the solution, steps and graphEnter your queries using plain English To avoid ambiguous queries, make sure to use parentheses where necessary Here are some examples illustrating how to ask for a derivative derivative of arcsin;
Then the x2 y2 z z tangent plane is z = z0 0 x0 (x−x y0 x0 x y0 y , since x2y2 = z2 0) (y−y0), or z =For the function z = x2y3 Solution z = x2y3 ∴ ∂z ∂x = 2xy3, and ∂z ∂y = x23y2, = 3x2y2 For the first part y3 is treated as a constant and the derivative of x2 with respect to x is 2x For the second part x2 is treated as a constant and the derivative of y3 with respect to is 3 2 Exercise 1 Find ∂z ∂x and ∂z ∂y for each ofDifferentiate (x^2 y)/(y^2 x) wrt x;
Lecture 9 Partial derivatives If f(x,y) is a function of two variables, then ∂ ∂x f(x,y) is defined as the derivative of the function g(x) = f(x,y), where y is considered a constant It is called partial derivative of f with respect to x The partial derivative with respect to y is defined similarly One also uses the short hand notationBy symmetry (interchanging x and y), zy = ;A graph of z = x 2 xy y 2 For the partial derivative at (1, 1) that leaves y constant, the corresponding tangent line is parallel to the xzplane A slice of the graph above showing the function in the xzplane at y = 1 Note that the two axes are shown here with different scales The slope of the tangent line is 3




Partial F X Y X F X X2 Y2 And Then We Evaluate The Derivative As If Y Is A Constant Pdf Free Download




1 Supplement Partial Derivatives 2 1 D Derivatives Review Given F X F X Df Dx Rate Of Change Of F At Point X W R T X H F X H F X Xx H Ppt Download
Partial Derivative Formulas and Identities There are some identities for partial derivatives as per the definition of the function 1 If u = f (x,y) and both x and y are differentiable of t ie x = g (t) and y = h (t), then the term differentiation becomes total differentiation 2 x2y2 = x2 ⋅ (some function)2 To differentiate this, you'd need the product rule and the chain rule d dx x2 ⋅ (some function)2 = 2x ⋅ (some function)2 x2 ⋅ 2(some function) ⋅ the derivative of the function That looks kinda complicated, but we have names for the some function and for its derivative We call them y and dy dx Explanation d dx (√x) = 1 2√x, so d dx (√u) = 1 2√u du dx d dx (√x2 y2) = 1 2√x2 y2 ⋅ d dx (x2 y2) = 1 2√x2 y2 (2x 2y dy dx) = 1 2√x2 y2 2x 1 2√x2 y2 2y dy dx = x √x2 y2 y √x2 y2 dy dx In order to solve for dy dx you will, of course, need the rest of the derivative of the rest of the original




Solved Find All The First Order Partial Derivatives For The Chegg Com



1
Answer to Let x^2 y^2 z^2 = 3xyz Find partial derivatives z_x, z_y By signing up, you'll get thousands of stepbystep solutions to your01 Recall ordinary derivatives If y is a function of x then dy dx is the derivative meaning the gradient (slope of the graph) or the rate of change withDerivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series \frac{\partial}{\partial x}(\frac{1}{(x^{2}y^{2}z^{2})}) en Related Symbolab blog posts Practice, practice, practice



Second Order Partial Derivatives In Calculus
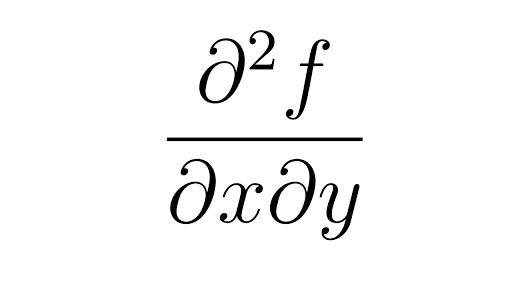



Second Partial Derivatives Article Khan Academy
Partial Derivatives of f(x;y) @f @x "partial derivative of f with respect to x" Easy to calculate just take the derivative of f wrt x thinking of y as a constant @f @y "partial derivative of f with respect to y" Christopher Croke Calculus 115 Examples Compute @f @x and @f @y for f (x;y) = 2x2 4xy (xy3 xy)3For each below, find the partial derivative of y with respect to x, and then find the partial derivative of y with respect to 2% a y = 10 4x?Partial derivative of sqrt (16x^2y^2) \square!



2




Locate The Stationary Points Of The Function F X Y X 2 2y 2 Exp X 2 Y 2 A 2 Where A Is A Non Zero Constant Sketch The Function Along The X And Y Axes And
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Derivative of arctanx at x=0;Answer to Find the first partial derivative of the following functions \\rm{f(x,y)=y cos({x}^{2} {y}^{2})} By signing up, you'll get thousands of



Solved Find All The First And Second Order Partial Derivatives Of F X Y X 2y 2 E Xy Sin X 2y Course Hero



Solved Determine The Second Partial Derivatives Of F X Y Z Tan 5 2x2y4z2 Xx 4y42 8x2y422tan 2x2y422 5 1 Sec 2x2y4 2 5 Course Hero
Free secondorder derivative calculator second order differentiation solver stepbystep This website uses cookies to ensure you get the best experienceIf you are taking the partial derivative with respect to y, you treat the others as a constant The derivative of a constant is 0, so it becomes 002x (3y^2) You'll notice since the last one is multiplied by Y, you treat it as a constant multiplied by the derivative of the function = ( y^2 z^2 ) / (x^2 y^2 z^2)^(3/2) But I can't for the life of me see where the square root went in the first term of the derivative I see how everything else is simplified, but how does that term suddenly become squared??



2



2
Answer to Find the partial derivative of the function u=e^{x^2y^2z^2} By signing up, you'll get thousands of stepbystep solutions to yourFree ebook http//tinyurlcom/EngMathYTI discuss and solve an example where we calculate the partial derivative of $\arctan (y/x)$ with respect to $x$ The m If you want to differentiate this expression as part of an implicit differentiation problem, here is how Assuming that we want to find the derivative with respect to x of xy^2 (assumong that y is a function of x First use the product rule d/dx(xy^2) = d/dx(x) y^2 x d/dx(y^2) Now for d/dx(y^2) we'll need the power and chain rules d/dx(xy^2) = 1 y^2 x 2y




Consider The Function F X Y Ln X 2 Y 2 3 Compute The Partial Derivatives Of The First And Second Order Mathematics Stack Exchange




Let F R2 R Be Given By Z Y 0 0 R Y 2y And F 0 0 Homeworklib
(delw)/(delx) = x/sqrt(x^2 y^2 z^2) (delw)/(dely) = y/sqrt(x^2 y^2 z^2) (delw)/(delz) = z/sqrt(x^2 y^2 z^2) Since you're dealing with a multivariable function, you must treat x, y, and z as independent variables and calculate the partial derivative of w, your dependent variable, with respect to x, y, and z There are two possible pathways here implicit differentiation or partial differentiation For implicit differentiation, we have both variables ( x and y) into the derivative at once, while for partial differentiation we work with each one separately Implicitly differetiating, then, we must resort to chain rule, by naming u = x2 y2 and, therefore, f x ( x 0, y 0) ( x − x 0) f y ( x 0, y 0) ( y − y 0) f ( x 0, y 0) is the z value of the point on the plane above ( x, y) Equation 1431 says that the z value of a point on the surface is equal to the z value of a point on the plane plus a "little bit,'' namely ϵ 1 Δ x ϵ 2 Δ y



Derivative Of Xy




Using Nabla With Partial Derivatives And The Laplace Operation Partial X 2 Partial Y 2 Partial Z 2 Mathematics Stack Exchange
Generalizing the second derivative Consider a function with a twodimensional input, such as Its partial derivatives and take in that same twodimensional input Therefore, we could also take the partial derivatives of the partial derivatives These are called second partial derivatives, and the notation is analogous to the notation for32 b y = 2x2 x 2z2 d y = 10 xz 2x z This problem has been solved!If u = f (x,y) 2 then, partial derivative of u with respect to x and y defined as u x = n f ( x, y) n – 1 u_ {x} = n\left f\left ( x,y \right ) \right ^ {n – 1} ux = nf (x,y)n–1 ∂ f ∂ x \frac {\partial f} {\partial x} ∂x∂f



What Is The Partial Derivative Of X 3y Xy 3 With Respect To X Quora




Question Video The Chain Rule For Multivariate Functions Nagwa
It's a bit wierd question but I have to ask it $$ \\text{Let }\\space f(x, y) = \\begin{cases} \\dfrac{xy}{x^2 y^2}, &Answer (1 of 2) This question is meaningless as you only define partial derivatives of a function f of more than one variables with respect to one of the specific variables among them If your function is given by f(x,y) = x for all (x,y), then (del f)/(del y) = 0, everywhere if the variable x2 PARTIAL DIFFERENTIATION 1 b) wx = −y2/x2, wy = 2y/x;



Math Wpi Edu




Solved Find All The Second Order Partial Derivatives Of The Chegg Com
Draw graph Edit expression Direct link to this page Value at x= Derivative Calculator computes derivatives of a function with respect to given variable using analytical differentiation and displays a stepbystep solution It allows to draw graphs ofAnswer (1 of 2) The context appears to be classical (Lagrangian) mechanics The overdot is just shorthand for differentiation with respect to time That is, \dot{x}\equiv dx/dt, for instance More importantly, what you are differentiating is the action In Lagrangian physics, the action is trePartial Derivative If u=x^2 tan^1 (y/x) y^2 tan^1 (x/y) Prove Ә^2u/ӘxӘy= (x^2y^2)/ (x^2y^2) Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly




Copyright C Cengage Learning All Rights Reserved Partial Derivatives Ppt Download



Solved Find The Indicated Partial Derivative F X Y Z Ln Dfrac 1 Sqrt X 2 Y 2 Z 2 1 Sqrt X 2 Y 2 Z 2 F Y 1 2 2
\\text{if $(x, y) \\ne (0,0)$} \\\\ 0Derivative x^2(xy)^2 = x^2y^2 Natural Language; Here is the work for this, h(y) =f (a,y) = 2a2y3 ⇒ h′(b) = 6a2b2 h ( y) = f ( a, y) = 2 a 2 y 3 ⇒ h ′ ( b) = 6 a 2 b 2 In this case we call h′(b) h ′ ( b) the partial derivative of f (x,y) f ( x, y) with respect to y y at (a,b) ( a, b) and we denote it as follows, f y(a,b) = 6a2b2 f y ( a, b) = 6 a 2 b 2




Answered 7 Find The Second Partial Derivatives Bartleby



Derivative Calculator With Steps
Partial Derivative The given function z consists of two variables x and y To find the partial derivative of the given function with respect to the variable y, differentiate the function withSee the answer See the answer See the answer done loadingTherefore at (1,2,4), we get wx = −4, wy = 4, so that the tangent plane is w = 4−4(x −1)4(y −2), or w = −4x 4y x x y 2B2 a) zx = = ;




Answered 36 6x2 Y2 2 Evaluate The Limit Using Bartleby



2
Derivative of x/(x^2y^2) by x = (y^2x^2)/(y^42*x^2*y^2x^4) Show a step by step solution;Let's first think about a function of one variable (x) f(x) = x 2 We can find its derivative using the Power Rule f'(x) = 2x But what about a function of two variables (x and y) f(x, y) = x 2 y 3 We can find its partial derivative with respect to x when we treat y as a constant (imagine y is a number like 7 or something) f' x = 2x 0 = 2xMixed Partial Derivatives f (x, y) = x2y3 f x = 2xy3 f y = 3x2y2 f xx = 2y3 f yx = 6xy2 f xy = 6xy2 f yy = 6x2y A mixed partial derivative has derivatives with respect to two or more variables f xy and f yx are mixed f xx and f yy are not mixed In this example, notice that f xy = f yx = 6xy2 The order of the derivatives did not affect the



2




2 Partial Differentiation
Lecture 9 Partial derivatives If f(x,y) is a function of two variables, then ∂ ∂x f(x,y) is defined as the derivative of the function g(x) = f(x,y), where y is considered a constant It is called partial derivative of f with respect to x The partial derivative with respect to y is defined similarly We also use the short hand notation Note that by the chain rule, $$\frac{d}{dy} \left(e^{ag(y) b}\right) = ae^{ag(y)b}\cdot g'(y)$$ Hence the partial derivative of $f(x,y,z)=e^{x^2 2y^2 3z^2}=e^{ag(y) b}$ with respect to $y$ is $$f_y(x,y,z)=2e^{x^2 2y^2 3z^2} \frac{\partial}{\partial y} (y^2)$$ where we applied the above rule with $a=2$, $g(y)=y^2$ and How to find partial derivative $\frac{u}{\sqrt{x^2 y^2}} \arctan\frac{u}{\sqrt{x^2 y^2}} 1 = 0$ 4 Finding the limit by using the definition of derivative




Formal Definition Of Partial Derivatives Video Khan Academy




Solved Find The Indicated Partial Derivative F X Y Z Ln Dfrac 1 Sqrt X 2 Y 2 Z 2 1 Sqrt X 2 Y 2 Z 2 F Y 1 2 2
There's a factor of 2 missing in all your second derivatives The result is exactly as you'd expect The variable you're differentiating with respect to, matters If it's x, then y is treated as a constant, and vice versa So if the "active" variable is leading in the numerator in one derivative, the same should apply in the other
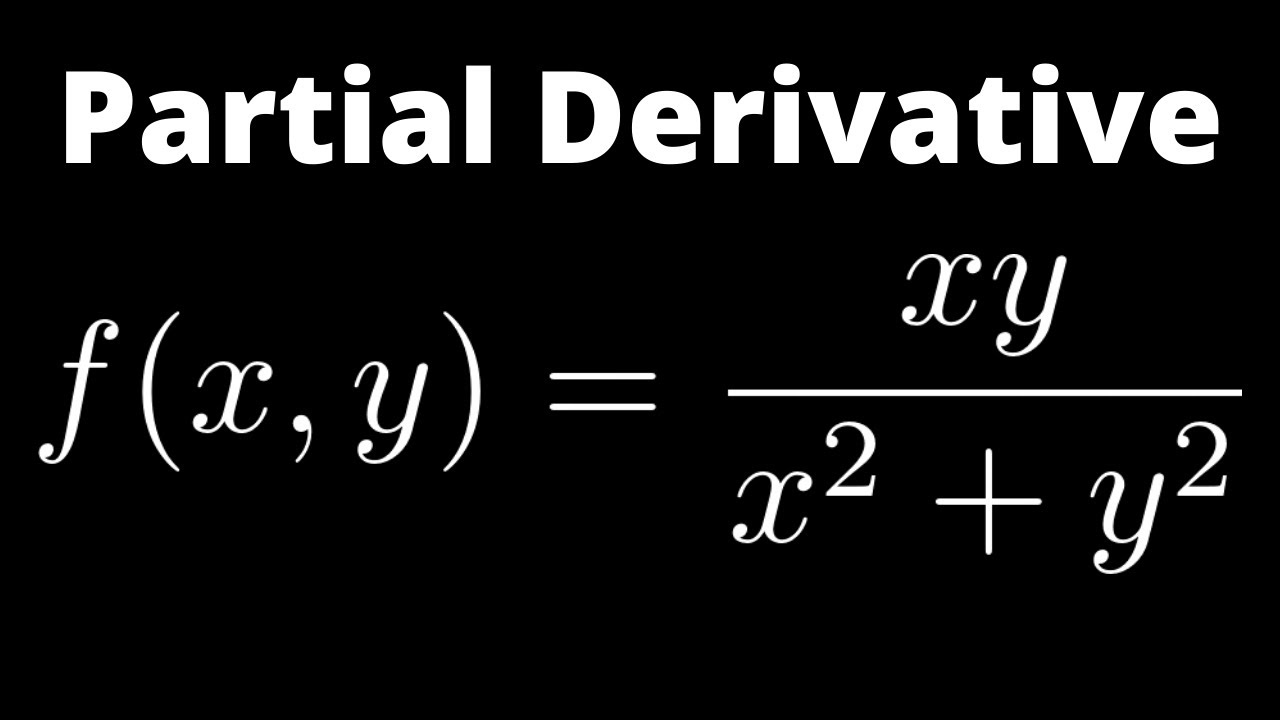



Partial Derivative Of F X Y Xy X 2 Y 2 With Quotient Rule Youtube



2




Copyright C Cengage Learning All Rights Reserved Partial Derivatives Ppt Download



1




Multivariate Functions And Partial Derivatives Sage Research Methods




Show That Xux Yuy Zuz 2u If U X 2 Y 2 Z 2 Partial Derivatives Solved Example Math Traders




Partial Derivatives Archives Www Tinspireapps Com Stepwise Math Science Solutions



Partial Derivative Calculator Symbolab



2




Solved Calculate The Second Order Partial Derivatives F X Chegg Com



Faculty Tarleton Edu




1 Partial Derivatives Of F X Y Xy Y Xy Are F Y 2xy Y
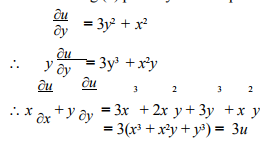



Partial Derivatives Differentiation Business Mathematics Statistics B Com Notes Edurev




Partial Derivatives Pdf Derivative Function Mathematics



2



What Is The Partial Derivative Of U Y X W R T To X And Y Quora
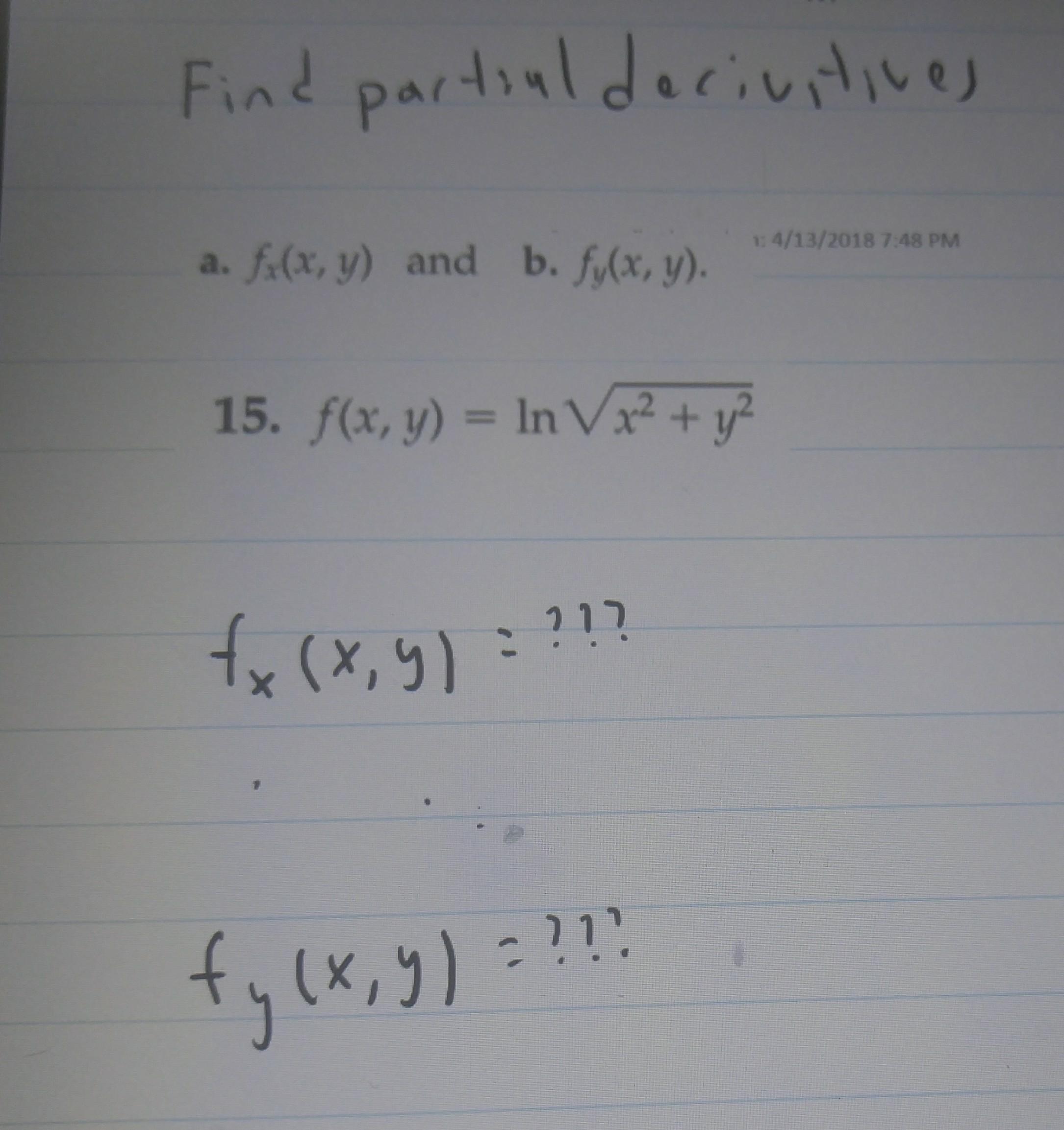



What Is The Partial Derivatives Of This Function Socratic




Solved Find All The First Order Partial Derivatives For The Chegg Com



17 5 Higher Order Partial Derivatives Graphing Calculator By Mathlab User Manual




Problems On Partial Differentiation U Log X 2 Y 2 Z 2 U Tan 1 2xy X 2 Y 2 Z F X Ay Q X Ay Youtube
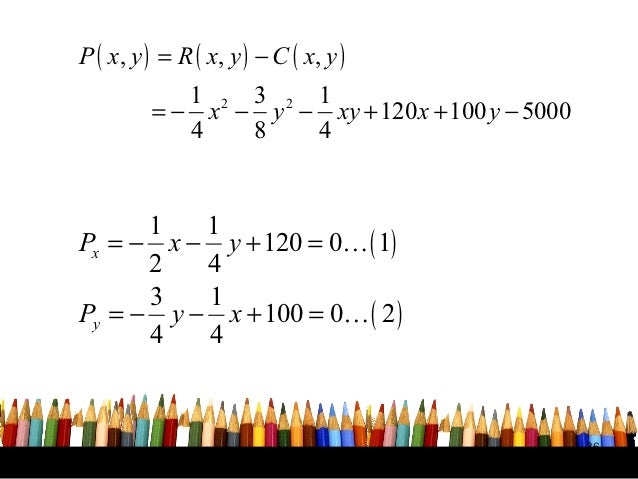



Partial Differentiation Application



Partial Derivatives




Doc Chapter Four Derivatives Of Multivariate Functions Partial Differentiation Habtamu Destaw Academia Edu
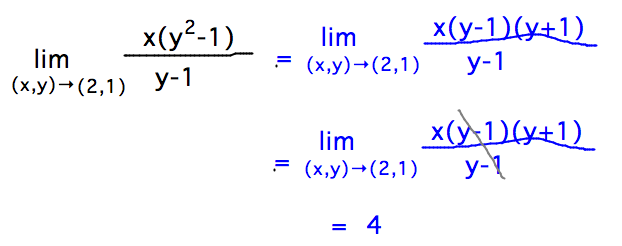



Geneseo Math 223 03 Partial Derivatives



12 3 Partial Derivatives Mathematics Libretexts




Second Order Partial Derivatives Ucsd Second



Definition Of Partial Derivative Page 128 129 Fx



1



Partial Derivatives




Use The Chain Rule To Find The Indicated Partial Derivatives I H2 Yz X Homeworklib




14 Partial Derivatives Partial Derivatives In Example 6




Pdf Functions Of Several Variables And Partial Di Erentiation 1 Functions Of Several Variables Mic Mus Academia Edu




Calc 501 1000 By James Bardo Issuu



2




Calculus 3 Partial Derivative 14 Of 30 Find More Partial Derivatives Example 2 Of 2 Youtube




Partial Derivative If U X 2 Tan 1 Y X Y 2 Tan 1 X Y Prove ә 2u әxәy X 2 Y 2 X 2 Y 2 Youtube




Derivative Of Log Confusion Mathematics Stack Exchange




Solved Find The First And Second Order Partial Derivatives Chegg Com




Multivariate Functions And Partial Derivatives Sage Research Methods




See Solution Compute The Partial Derivative F X For F X Y 2y E 2x 1195




Derivative Calculator Wolfram Alpha




Applications Of Partial Derivatives Use The Chain Rule To Find Dz Dt Z X 2 Y 2 Xy X Sin T Y 3e T Wegglab



Find The Partial Derivatives Of The Following Functions At The Indicated Points I F X Y 3x 2 2xy Y 2 5x 2 2 5 Sarthaks Econnect Largest Online Education Community



2




Partial Derivative Examples Math Insight




Ppt 5 1 Definition Of The Partial Derivative Powerpoint Presentation Id




Answered Homework 3 Due Tuesday November 27th Bartleby




Using The Appropriate Properties Of Ordinary Derivatives Perform The Following A Find All The First Partial Derivatives Of The Following Functions F X Y I X 2 Y Ii X 2 Y 2 4 Iii Sin X Y Iv Tan



Compute Partial Derivatives Of The Given Function Stumbling Robot




Maxima And Minima
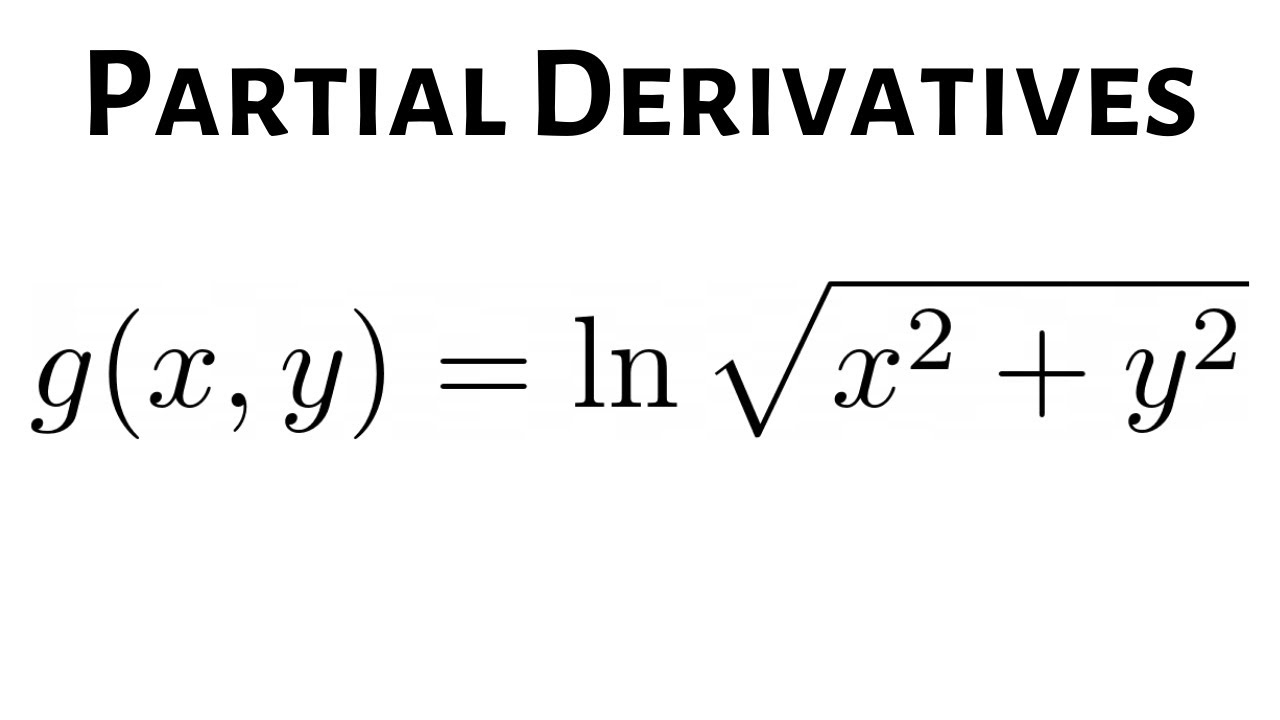



Larson Calculus 13 3 28 First Partial Derivatives Of G X Y Ln Sqrt X 2 Y 2 Youtube




Solved F X Y Z X 2y Y 2z Xz 2 Partial Differential Chegg Com



Solved Find All The First And Second Order Partial Derivatives Of F X Y X 2y 2 E Xy Sin X 2y Course Hero



2
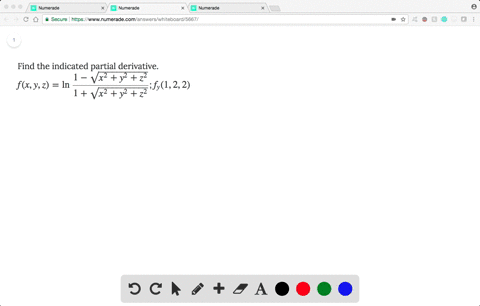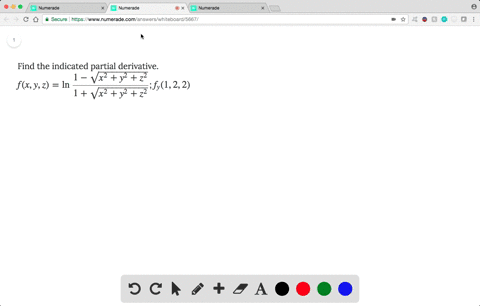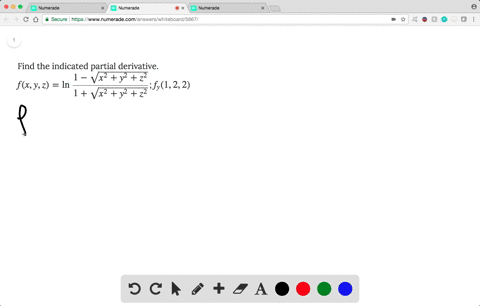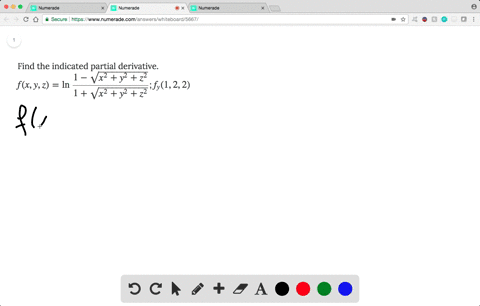



Solved Find The Indicated Partial Derivative F X Y Z Ln Dfrac 1 Sqrt X 2 Y 2 Z 2 1 Sqrt X 2 Y 2 Z 2 F Y 1 2 2




Derivative Calculator Wolfram Alpha




Second Order Partial Derivatives F X Y Sqrt X 2 Y 2 Youtube



2



2




Partial Derivative Math Help Forum
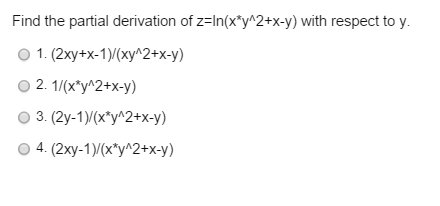



Solved Find The Partial Derivative Of F X Y E X2 Y2 With Chegg Com




Review Of Partial Derivatives Bruce E Shapiro




Copyright C Cengage Learning All Rights Reserved Partial Derivatives Ppt Download



If U 2 1 X 2 Y 2 Z 2 Then Show That 2u X 2 2u Y 2 2u Z 2 0 Sarthaks Econnect Largest Online Education Community
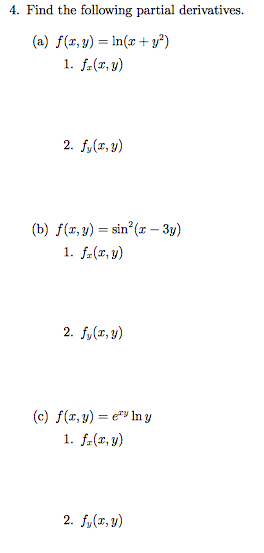



Solved 4 Find The Following Partial Derivatives A Chegg Com




Partial Derivative Of F X Y Z With Respect To Z Mathematics Stack Exchange



Multivariable Partial Derivative Dp



Rules Of Calculus Multivariate




Partial Differentiation Application Ppt Download




Step By Step Partial Derivative Solution Sample
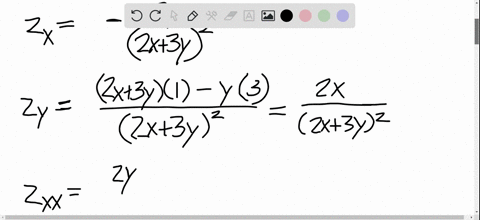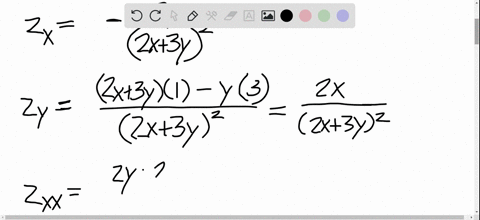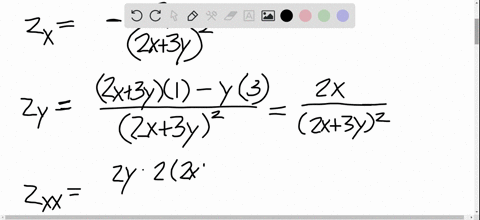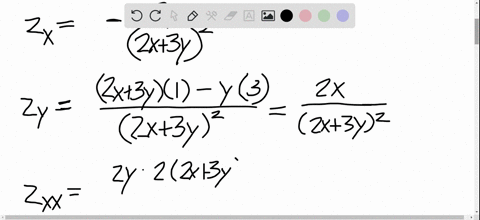



Solved Find All The Second Partial Derivatives Z Dfrac Y 2x 3y




Partial Differentiation If Z X Y X 2 Y 2 Show That әz әx әz әy 2 4 1 әz әx әz әy Youtube




Partial Derivative Examples Math Insight



Partial Derivatives Calculus Volume 3



0 件のコメント:
コメントを投稿